sleca

Le site

Nombres complexes

Définitions Opérations Module et argument Interprétation géométrique

Transformations Trigonométrie Equations du second degré Méthodes et exercices

DEFINITIONS

Un nombre complexe z est un nombre de la forme x+iy, où x et y sont deux réels et i est un nombre imaginaire vérifiant i²=-1.

cette écriture est appelée forme algébrique de z

L'ensemble des nombres complexes est noté `CC` .

x est la partie réelle de z, notée Re(z)

y est la partie imaginaire de z, notée Im(z)

Attention: x et y sont des réels

z est réel si et seulement si Im(z)=0

z est imaginaire pur si et seulement si Re(z)=0

z=z' si et seulement si `{(Re(z)=Re(z')),(Im(z)=Im(z')):}`
Dans un plan muni d'un repère orthonormé direct `(O;vec(u),vec(v))`, appelé plan complexe :
le nombre complexe x+iy est l'affixe du point M(x;y) ou du vecteur `vec(OM)` ;

on écrit x+iy=`z_(M)` `=` `z_(vec(OM))` ou encore M(x+iy)

(Ox) est l'axe réel

(Oy) est l'axe imaginaire.
Pour tout nombre complexe z de forme algébrique x+iy, on appelle conjugué de z le nombre complexe x-iy, noté `barz` .
Le point M₁(`barz` ) est le symétrique de M(z) par rapport à l'axe des abscisses (Ox)

Un nombre complexe et son conjugué ont même partie réelle et des parties imaginaires opposées

OPERATIONS SUR LES NOMBRES COMPLEXES

Somme, produit, quotient

z=x+iy, z'=x'+iy', k réel

z+z'=(x+x') + i(y+y')

k.z= (kx) + i(ky)

zz'= (xx'-yy') + i(xy'+x'y)

remarque: en pratique on effectue les calculs en appliquant les règles habituelles dans `RR` et en remplaçant i² par -1

`1/z=(barz)/(zbarz)`=`x/(x^2+y^2)-i y/(x^2+y^2)`

`(z')/z=z'xx1/z`
en pratique pour mettre `(z')/z` sous forme algébrique, on multiplie numérateur et dénominateur par le conjugué `barz` de z

Propriétés du conjugué:

`barbarz=z` ; `z+barz=2xxRe(z)` ; `z-barz=2ixxIm(z)` ;

z réel ssi `barz=z`

z imaginaire pur ssi `barz=-z`

`bar(z+z')=barz+barz'` ; `bar(zz')=barzxxbarz'` ; si z`!=` 0, `bar((1/z))=1/barz` et `bar(((z')/z))=bar(z')/barz`

MODULE ET ARGUMENT

Définitions:

Soit M(z) dans le plan complexe avec z=x+iy, z non nul

OM=|z|=`sqrt(x^2+y^2)` |z|est appelé module de z (|0|existe et vaut 0...)

`(vecu;vecOM)=theta +2kpi` `theta` est un argument de z (0 n'a pas d'argument)

(|z|; `theta` ) sont les coordonnées polaires de M dans (O; `vecu` )

soit z complexe non nul,

la forme algébrique de z est z= x+iy

la forme trigonométrique de z est z= |z|(cos`theta``theta` ) +isin

et on a: x=|z|cos`theta` et y=|z|sin`theta`

Propriétés:

pour z et z' non nuls, k entier

z=z' ssi `{(|z|=|z'|),(arg(z)=arg(z')+2kpi):}`

`|zz'|=|z|xx|z'|` ; `arg(zz')=arg(z)+arg(z') + 2kpi` , kentier

`|1/z|=1/|z|` et `arg(1/z)=- arg(z) +2kpi`

`|z/(z')|=(|z|)/(|z'|)` et `arg(z/(z'))=arg(z)-arg(z') +2kpi`

`|barz|=|z|=|-z|` et `{(arg(barz)=-arg(z) ),(arg(-z)=arg(z)+pi ):}` (mod `2pi` )

INTERPRETATION GEOMETRIQUE

A,B,C trois points distincts deux à deux d'affixes respectives z_A, z_B , z_C

alors:|zB-zA|=AB et arg(z_B-z_A)=`(vecu,vec(AB))` `+ 2kpi` (1)

`|(z_B-z_C)/(z_A-z_C)|=(CB)/(CA)` et `arg((z_B-z_C)/(z_A-z_C))=(vec(CA),vec(CB)) + 2kpi` (2)

démonstration:

pour (1): introduire M tel que `vec(OM)=vec(AB)` donc `z_M=z_B-z_A`

pour (2): on utilise le module d'un quotient...

puis :`arg((z_B-z_C)/(z_A-z_C))=arg(z_B-z_C)-arg(z_A-z_C)=(vecu,vec(CB))-(vecu,vec(CA))`

`=(vecu,vec(CB))+(vec(CA),vecu)=(vec(CA),vec(CB)) + 2kpi`

TRANSFORMATIONS DU PLAN

Soit une transformation F du plan qui à tout point M d'affixe z associe le point M' d'affixe z'.

On appelle fonction complexe associée à F, la fonction f de `CC` dans `CC` qui à z associe z'.

Translation: t translation de vecteur `vecu` d'affixe b

`t(M)=M' hArr vec(MM')=vecu hArr z'=z+b`

Homothétie: h homothétie de centre `Omega`(`omega` ) et de rapport k (k réel non nul)

`h(M)=M'hArr vec(OmegaM')=kvec(OmegaM) hArr z'-omega=k(z-omega) `

Cas particulier: si `Omega=O` alors on obtient simplement : z'=kz

Rotation: r rotation de centre `Omega(omega)` et d'angle `theta`

pour` M!=Omega` :

`r(M)=M' hArr OmegaM=OmegaM' et (vec(OmegaM),vec(OmegaM'))=theta `

`hArr |(z'-omega)/(z-omega)|=1` et `arg((z'-omega)/(z-omega))=theta `

` hArr (z'-omega)/(z-omega)=e^(itheta)`

` hArr z'-omega=e^(itheta)(z-omega)`

pour `M=Omega` on a `r(M)=M= Omega` et l'égalité précédente reste vraie

Cas particulier: si `Omega=O` alors on obtient simplement : `z'= e^(itheta)z`

APPLICATIONS A LA TRIGONOMETRIE

Formule de Moivre:

Pour tout réel `theta` et tout entier n on a: `(costheta+isintheta)^n=cosntheta+isinntheta`

Formules d'Euler:

Pour tout nombre réel `theta` on a: `e^(itheta)=costheta+isintheta` et `e^(-itheta)=costheta-isintheta`

d'où: `costheta=(e^(itheta)+e^(-itheta))/2` et `sintheta=(e^(itheta)-e^(-itheta))/(2i)`

Ces formules sont utilisées pour des problèmes de linéarisation (exprimer `cos^ntheta` ou `sin^ntheta` sous forme de sommes de termes de la forme: `acos(mtheta)` et `bsin(ptheta)` ..)

EQUATIONS DU SECOND DEGRE À COEFFICIENTS REELS

Formules de résolution:

a, b, c étant trois réels donnés avec a non nul, on pose: `Delta =b^2-4ac`

Dans `CC` , l'équation az²+bz+c =0 admet toujours deux solutions (confondues si `Delta=0` ):

`z_1=(-b-delta)/(2a)` et `z_2=(-b+delta)/(2a)`

où `delta` est un nombre complexe dont le carré est le discriminant: `delta^2=Delta`

METHODES

Comment utiliser les différentes formes d'un nombre complexe

Forme algébrique

a+ib

Vérifier que a et b sont des réels

Facilite les calculs de somme et de différence
Permet de faire le lien entre les complexes et les coordonnées cartésiennes

Forme trigonométrique

r(cosθ+isinθ)

Vérifier que r est positif

Etablit un lien entre les complexes et la géométrie et permet les calculs de distances et d'angles

Forme exponentielle

`re^(itheta)`

Vérifier que r est positif

Facilite les calculs de produits, de quotients et de puissances de nombres complexes

Ex1: Relier les nombres complexes à leurs différentes formes

Complexes	Forme algébrique	Forme trigonométrique	Forme exponentielle
`(1+i)^3`	-2-2i	`2sqrt(2)(cos(pi/4)+isin(pi/4))`	`sqrt(2)e^(i(3pi)/4)`
`-2sqrt(2)(cos(pi/4)+isin(pi/4))`	2+i	`2sqrt(2)(cos((3pi)/4)+isin((3pi)/4))`	`2sqrt(2)e^(-i(3pi)/4)`
`(8+4i)/(3-i)`	-2+2i	`2sqrt(2)(cos(-(3pi)/4)+isin(-(3pi)/4))`	`2sqrt(2)e^(ipi/4)`

Comment identifier des complexes particuliers

Pour prouver que z est un ....	réel	imaginaire pur
on peut prouver que....	soit Im(z)=0 soit `barz=z` soit arg(z)=0 (`pi` ) ou z=0	soit Re(z)=0 soit `barz=-z` soit arg(z)=`pi/2` (`pi` ) ou z=0

Ex2: Pour tout complexe z différent de 1+i, on associe le complexe `z'= (z-2i)/(z-1-i)`

Déterminer l'ensemble des points M d'affixe z tels que:

a) z' soit un réel non nul

b) z' soit un imaginaire pur non nul

(utiliser les arguments)

Ex3: Pour tout complexe z différent de 1+i, on associe le complexe `z'=(2z-2i)/(z-1-i)`

On pose z=x+iy et z'=x'+iy'

Déterminer l'ensemble des points M d'affixe z tels que:

a) z' soit un réel

b) z' soit un imaginaire pur

Comment préciser la position relative de trois points

Dans le plan complexe, z_A, z_B et z_C sont trois nombres complexes distincts, d'images respectives A, B, C. On note `Z=((z_C-z_B)/(z_B-z_A))`

La condition:	équivaut à:
\|Z\|=1	AB=AC
Z est un réel	A, B, C sont alignés
Z est un imaginaire pur	(AB) et (AC) sont perpendiculaires
Z=`+-` i	ABC est rectangle et isocèle de sommet A
`Z=e^(+-ipi/3)`	ABC est un triangle équilatéral

Ex4: Que peut on dire des points A, B et C dans les cas suivants?

a) z_A=2+i; z_B=1-i; z_C=2+2i c) z_A=-1+i`sqrt(3)` ; z_B=-1-i`sqrt(3)` ; z_C=2

b) z_A=2+i; z_B=1+i; z_C=1-i d) z_A=-1-2i; z_B=-10-8i; z_C=2

Comment utiliser les transformations

On identifie la transformation étudiée	T est la translation de vecteur `vecu`	H est l'homothétie de centre `Omega` et de rapport k non nul	R est la rotation de centre `Omega` et d'angle `theta`
On détermine l'écriture complexe associée	`vecu` est un vecteur d'affixe b `z'=z+b`	`Omega` est le point d'affixe `omega` `z'-omega =k(z-omega )`	`Omega` est le point d'affixe `omega` `z'-omega=e^(itheta)(z-omega)`

Ex5: Trouver pour chaque transformation son écriture complexe.

(1) Homothétie de centre `Omega` (-1+2i) et de rapport -2	(A) ` z'=iz+1+3i`
(2) Rotation de centre `Omega` (-1+2i) et d'angle `pi/2`	(B) `z'=e^(ipi/4)z+(1/2-1/2i)sqrt(2)+i`
(3) Homothétie de centre `Omega` (i) et de rapport `sqrt(2)`	(C) `z'=z-1+2i`
(4) Translation de vecteur `vecu` (-1+2i)	(D) `z'=-2z-3+6i`
(5) Rotation de centre `Omega` (i) et d'angle `pi/4`	(E) `z'=sqrt(2)z+i(1-sqrt(2))`

Ex6: On considère les points A et B d'affixes z_A=2+i et z_B=6+3i

À tout point M d'affixe z, on associe le point M' d'affixe z'=iz+2 et on note f(M)=M'

1) Déterminer la nature et les éléments caractéristiques de f

2) Déterminer les affixes z_C et z_D des points C et D tels que f(A)=C et f(B)=D

3) Montrer que la rotation de centre J d'affixe 3+5i et d'angle - `pi/2` transforme A en D
et B en C

correction ex6:

1) on cherche s'il y a un point invariant `Omega(omega)`

on a `omega=iomega+2`

donc

`omega=2/(1-i)=1+i `

On en déduit : `z'-omega=i(z-omega)`

donc f est la rotation de centre `Omega` et d'angle `arg(i)=pi/2`

2) `z_C=i(2+i-1-i)+1+i=2i+1` et ` z_D=i(6+3i-1-i)+1+i=6i-1`

3) r rotation de centre J et d'angle `pi/2`

son écriture complexe est: `z'=3+5i-i(z-3-5i)`

`z'_A=3+5i-i(2+i-3-5i)=-1+6i=z_D`

`z'_B=3+5i-i(6+3i-3-5i)=1+2i=z_C`

Exercice de cours du mardi 12/01

Résoudre dans `CC` l'équation: `z^2+4z+16=0`

`Delta` =-48 donc deux racines complexes conjuguées `z_1=-2+2isqrt(3)` et `z_2=-2-2isqrt(3)`

On prend A(`z_1` ), B(`z_2` )

Calculer l'affixe `z_3` du point C tel que ABC soit équilatéral direct

C est donc l'image de B par la rotation de centre A et d'angle `pi` /3

`z_3-z_1=e^(ipi/3)(z_2-z_1) `

donc `z_3=-2+2isqrt(3)+(1/2+isqrt(3)/2)(-4isqrt(3))=4`

(remarque on pouvait prévoir que C serait sur la médiatrice de [AB])

Calculer le périmètre P et l'aire S de ABC

P= 3 AB =3 |`z_2-z_1` |=3 |-4i`sqrt(3)` |=12`sqrt(3)`

`S= 1/2AB^2xx sqrt(3)/2=12sqrt(3)` (rappel: hauteur d'un triangle équilatéral de côté a = a`sqrt(3)/2` )

(remarque, ici, la hauteur vaut 6 ce qui se lit facilement sur un graphique!)

f est l'application d'écriture complexe z'=z-i

Reconnaitre f

f est la translation de vecteur `vecu(-i)`

Calculer l'affixe du point D tel que f(A)=D et celle du point E tel que f(E)=C

`z_D= -2+ 2isqrt(3)-i=-2+i(2sqrt(3)-1) `

4=`z_E-i` donc `z_E` =4+i

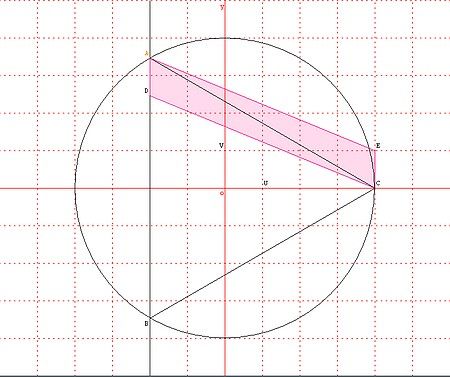
Quelle est la nature du quadrilatère ADCE et quelle est son aire?

ADCE parallélogramme car: `vec(AD)=vec(EC)=vecu`

aire(ADCE)= `ADxx6=6`