spécialité: sections planes

France, juin 2003

Les questions 3. et 4. sont indépendantes des questions 1.et 2. ; seule l’équation de Γ donnée en 1.c. intervient à la question 4.

1.  L’espace est rapporté au repère orthonormal

1. a.  Montrer que les plans P et Q d'équations et   2x-z=0   ne sont pas parallèles.

1. b.  Donner un système d’équations paramétriques de la droite D intersection des plans P et Q.

1. c.  On considère le cône de révolution Γ d’axe (Ox) contenant la droite D comme génératrice. Montrer que Γ a pour équation cartésienne : 

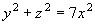
2.  On a représenté sur les deux figures ci-dessous les intersections de Γ avec des plans parallèles aux axes de coordonnées.

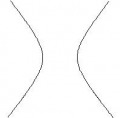
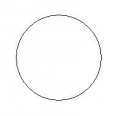
                                Figure 1                                                    Figure   2                      

Déterminer dans chaque cas une équation des plans possibles, en justifiant avec soin votre réponse.

3. a.  Montrer que l'équation:  , dont l’inconnue x est un entier relatif, n’a pas de solution.

3. b.  Montrer la propriété suivante : pour tous entiers relatifs a et b, si 7 divise a et 7 divise b.  alors 7 divise a²+b²

4. a.  Soient a, b et c des entiers relatifs non nuls. Montrer la propriété suivante : si le point A de coordonnées (a, b, c) est un point du cône Γ alors, a, b et c sont divisibles par 7.

4. b.  En déduire que le seul point de Γ dont les coordonnées sont des entiers relatifs est le sommet de ce cône.